Sortowanie przez scalanie
Sortowanie przez scalanie wykorzystuje metodę połowienia zbioru danych wejściowych (dziel i zwyciężaj). Ten typ sortowania jest dużo wydajniejszy niż sortowanie bąbelkowe, sortowanie przez wstawianie czy sortowanie przez selekcję, których złożoność jest kwadratowa O(n)2. Sortowanie przez scalanie cechuje złożoność logarytmiczna O(n⋅log2 n).
Wadą tego rozwiązania jest stosowanie pamięci buforowej dla kopii zbioru wejściowego, co podwaja zapotrzebowanie na pamięć przy sortowaniu. Nie jest to obojętne dla bardzo dużych zbiorów danych.
Ideę sortowania przez scalanie (merge sort) przedstawia poniższa ilustracja

źródło pl.wikipedia.org
Algorytm dzieli dane wejściowe na dwie równe części, każda z części kopiuje do tablicy buforowej. Dla każdej z tych części stosuje oddzielne sortowanie, po czym scala posortowane elementy w jeden posortowany zbiór. Kroki są rekurencyjnie wywoływane, dopóki nie osiągnięto jednoelementowego zbioru wynikającego z podziału.
Schemat algorytmu sortowania przez scalanie
Schemat przedstawia rekurencyjne rozwiązanie

Kod funkcji sortującej przez scalanie
Wskazówka:
void sortScalanie(Int32[] t, Int32[] tB, int L,int P)
{
//L, P- lewy i prawy zakres sortowanego przedzialu
if (P <= L) return;
//srodek zbioru
int sr = (P + L) / 2;
//podziel zbior na dwie czesci
//rekurencyjne wykonanie sortowania
sortScalanie(t,tB, L, sr);
sortScalanie(t,tB, sr+1, P);
//scal dwie sortowane tablice
int i, j;
//Lewą część zbioru przenies do bufora
for (i = sr + 1; i > L; i--)
tB[i - 1] = t[i - 1];
//Prawą część zbioru przenies do bufora
for (j = sr; j < P; j++)
tB[P+sr - j] = t[j + 1];
//scal obie tablice buforowe
//w tablicę zbioru posortowanego
for (int k = L; k <= P; k++)
if (tB[j] < tB[i])//test sortowania
t[k] = tB[j--];
else
t[k] = tB[i++];
//działanie kończy się w rekurencyjnym wywołaniu
//gdy L<=P
}
Aplikacja działa na zbiorze o podanym rozmiarze z wylosowanych elementów. Losowanie dopuszcza powtórzenia wylosowanych wartości. Patrz poniższa funkcja losująca
Losowanie z powtórzeniami:
void losujTablice(Int32[] t, int zakres)
{
Random r = new Random();
int i = 0;
//mogą występować powtórzenia wylosowanych elementów
while (i < t.Length)
{
t[i] = r.Next(zakres) + 1;
i++;
}
}
Przykładowa aplikacja wykorzystująca algorytm sortowania przez scalanie
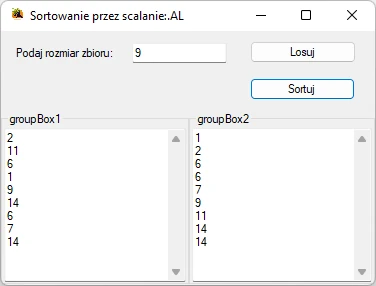
Pełny kod klasy Form utworzonej formatki aplikacji sortującej przez scalania
Form1.cs
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using static System.Windows.Forms.VisualStyles.VisualStyleElement;
namespace _13AlgSortScalanie
{
public partial class Form1 : Form
{
Int32[] tab1, //tablica glowna
tabBufor;//tablica pomocnicza
int rozmiar;//rozmiar zbioru
void losujTablice(Int32[] t, int zakres)
{
Random r = new Random();
int i = 0;
//mogą występować powtórzenia wylosowanych elementów
while (i < t.Length)
{
t[i] = r.Next(zakres) + 1;
i++;
}
}
void sortScalanie(Int32[] t, Int32[] tB, int L,int P)
{
//L, P- lewy i prawy zakres sortowanego przedzialu
if (P <= L) return;
//srodek zbioru
int sr = (P + L) / 2;
//podziel zbior na dwie czesci
//rekurencyjne wykonanie sortowania
sortScalanie(t,tB, L, sr);
sortScalanie(t,tB, sr+1, P);
//scal dwie sortowane tablice
int i, j;
//Lewą część zbioru przenies do bufora
for (i = sr + 1; i > L; i--)
tB[i - 1] = t[i - 1];
//Prawą część zbioru przenies do bufora
for (j = sr; j < P; j++)
tB[P+sr - j] = t[j + 1];
//scal obie tablice buforowe
//w tablicę zbioru posortowanego
for (int k = L; k <= P; k++)
if (tB[j] < tB[i])//test sortowania
t[k] = tB[j--];
else
t[k] = tB[i++];
//działanie kończy się w rekurencyjnym wywołaniu
//gdy L<=P
}
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
//losowanie nowej tablicy
if (textBox3.Text.Length < 1) return;
//wyczysc stara tablice
if (tab1 != null) Array.Clear(tab1, 0, tab1.Length);
if (tabBufor != null) Array.Clear(tabBufor, 0, tabBufor.Length);
//ustaw nowy rozmiar
rozmiar = int.Parse(textBox3.Text);
tab1 = new int[rozmiar];
tabBufor = new int[rozmiar];
//przy losowaniu ustaw zakres na 2 razy większy od rozmiaru
losujTablice(tab1, 2 * rozmiar);
//pokaz wylosowany zbior
textBox1.Clear();
for (int i = 0; i < tab1.Length; i++)
textBox1.AppendText(tab1[i].ToString() + Environment.NewLine);
}
private void button2_Click(object sender, EventArgs e)
{
if (tab1 == null) return;
sortScalanie(tab1, tabBufor, 0, rozmiar - 1);
//wypisz posortowaną
textBox2.Clear();
for (int i = 0; i < tab1.Length; i++)
textBox2.AppendText(tab1[i].ToString() + Environment.NewLine);
}
private void textBox3_KeyPress(object sender, KeyPressEventArgs e)
{
if (e.KeyChar == 8) return;//wyskocz na Backspace
if (e.KeyChar < '0' || e.KeyChar > '9') e.Handled = true;//ignoruj nienumeryczne
}
}
}









