Największy wspólny dzielnik (NWD) algorytm Euklidesa
Największy wspólny dzielnik (NWD), to wartość takiej liczby, która dzieli obie liczby bez reszty i jest możliwie największa ze wszystkich dzielników obu liczb. Taka liczba często jest wykorzystywana przy skracaniu ułamków. Wyznaczenie największego wspólnego dzielnik było po raz pierwszy opisane około 300 lat przed nasza era przez Euklidesa- stąd nazwa tego algorytmu.
Optymalny algorytm Euklidesa w swym działaniu wykorzystuje dzielenie z resztą na przemian kolejnych par liczb. Po pierwszym przejściu algorytmu nową parę tworzą wyznaczone reszty. Dzielenie trwa do momentu otrzymania reszty z dzielenia równej zero
Przykład wyznaczenia NWD dla pary liczb 18 i 12 (operator mod oznacza resztę z dzielenia)
18 mod 12 =6
12 mod 18 = 12
12 mod 6 = 0
Zauważamy, że reszta z dzielenia wynosi 0 przy dzieleniu przez 6. Stąd NWD dla pary liczb (18, 12) jest liczba 6.
Schemat algorytmu wyznaczającego największy wspólny dzielnik- metoda iteracyjna

Kod funkcji realizującej wyznaczenie NWD metodą iteracyjną podany jest poniżej
Wskazówka:
int iteracjaNWD(int a, int b)
{
//a to licznik, b to mianownik
int bufor;
while (b != 0)
{
bufor = b;//zapamietaj stary mianownik
b = a % b;//oblicz nowy na podstawie reszty
a=bufor;//zamien stary licznik na nowy ze starego mianownika
}
return a;//a jest NWD
}
Schemat algorytmu wyznaczającego największy wspólny dzielnik- metoda rekurencyjna

Kod funkcji realizującej wyznaczenie NWD metodą rekurencyjną podany jest poniżej
Wskazówka:
int rekurencjaNWD(int a, int b)
{
//a to licznik, b to mianownik
//reszta z dzielenia jest drugim argumentem
//w rekurencyjnym wywołaniu funkcj
if(b!=0)return rekurencjaNWD(b,a%b);
return a;
}
Przykładowa aplikacja wyznaczająca największy wspólny dzielnik algorytmem Euklidesa
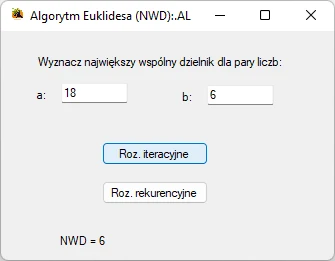
Pełny kod klasy Form utworzonej formatki aplikacji
Wskazówka:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace _5AlgEuklidesa_NWD
{
public partial class Form1 : Form
{
int iteracjaNWD(int a, int b)
{
//a to licznik, b to mianownik
int bufor;
while (b != 0)
{
bufor = b;//zapamietaj stary mianownik
b = a % b;//oblicz nowy na podstawie reszty
a=bufor;//zamien stary licznik na nowy ze starego mianownika
}
return a;//a jest NWD
}
int rekurencjaNWD(int a, int b)
{
//a to licznik, b to mianownik
//reszta z dzielenia jest drugim argumentem
//w rekurencyjnym wywołaniu funkcj
if(b!=0)return rekurencjaNWD(b,a%b);
return a;
}
public Form1()
{
InitializeComponent();
}
private void textBox1_KeyPress(object sender, KeyPressEventArgs e)
{
if (e.KeyChar == 8) return;//wyskocz jak BackSpace
if(e.KeyChar<'0'||e.KeyChar>'9') e.Handled=true;
}
private void button1_Click(object sender, EventArgs e)
{
int a = Int16.Parse(textBox1.Text),
b = Int16.Parse(textBox2.Text);
label4.Text="NWD = "+iteracjaNWD(a,b).ToString();
}
private void button2_Click(object sender, EventArgs e)
{
int a = Int16.Parse(textBox1.Text),
b = Int16.Parse(textBox2.Text);
label4.Text="NWD = "+rekurencjaNWD(a,b).ToString();
}
}
}









