Czy liczba jest liczbą doskonałą?
Liczba doskonała, to liczba, której suma jej dzielników właściwych (bez niej samej) jest jej równa.
Na przykład liczba 28 ma takie kolejne dzielniki właściwe 1, 2, 4, 7 i 14. Jeżeli obliczymy sumę tych dzielników
Suma=1 + 2+ 4 +7 +14 =14 + 14 =28
To widzimy, że obliczona wartość sumy jest równa badanej liczbie
Algorytm sprawdzający czy liczba jest liczbą doskonałą można opisać poniższą listą kroków
- ustaw zmienną suma dzielników na 1
- oblicz pierwiastek kwadratowy podanej liczby i zaokrąglij w dół
- dla każdej liczby od i=2 do zaokrąglonego pierwiastka w dół, sprawdzaj czy i-ta liczba jest dzielnikiem podanej liczby, jeśli tak to do sumy dzielników dodaj dwa dzielniki suma=suma + i+n/i
- gdy liczba jest kwadratowa n==p*p to od sumy odejmij jeden pierwiastek suma = suma ? p
- sprawdź czy suma jest równa podanej liczbie, jeśli tak, to jest to liczba doskonała
Schemat algorytmu liczby doskonałej

Kod funkcji realizującej algorytm sprawdzający czy liczba jest liczbą doskonałą
Wskazówka:
private bool czy_jest_doskonala(long n)
{
long suma = 1,//stan początkowy sumy
p = (long)Math.Floor(Math.Sqrt(n));//pierwiastek z podanej liczby
//szukaj w zakresie do pierwiastka z podanej liczby
for (long i = 2; i <= p; i++)
if (n % i == 0)//czy dzielnik
suma += i + n / i;//jak tak to dodaj dwa dzielniki
//sprawdz czy była to liczba kwadratowa
//jak tak, to odejmij pierwiastek, bo go wczśniej dodaliśmy dwa razy
if (n == p * p) suma -= p;
//gdy suma dzielnikow jest rowna liczbie to doskonla
if(n==suma)return true;
return false;
}
Przykładowa aplikacja badająca doskonałość liczb
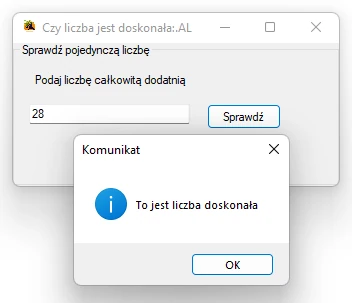
Pełny kod klasy Form utworzonej formatki aplikacji
Form.cs
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace _3AlgCzyLiczbaDoskonala
{
public partial class Form1 : Form
{
private bool czy_jest_doskonala(long n)
{
long suma = 1,//stan początkowy sumy
p = (long)Math.Floor(Math.Sqrt(n));//pierwiastek z podanje liczby
//szukaj w zakresie do pierwiastka z podanje liczby
for (long i = 2; i <= p; i++)
if (n % i == 0)//czy dzielnik
suma += i + n / i;//jak tak to dodaj dwa dzielniki
//sprawdz czy była to liczba kwadratowa
//jak tak, to odejmij pierwiastek, bo go wczśniej dodaliśmy dwa razy
if (n == p * p) suma -= p;
//gdy suma dzielnikow jest rowna liczbie to doskonla
if(n==suma)return true;
return false;
}
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
if (textBox1.Text.Length < 1) return;
long n=Int64.Parse(textBox1.Text);
if (czy_jest_doskonala(n))
MessageBox.Show(
"To jest liczba doskonała",
"Komunikat",
MessageBoxButtons.OK,
MessageBoxIcon.Information
);
else MessageBox.Show(
"To nie jest liczba doskonała",
"Komunikat",
MessageBoxButtons.OK,
MessageBoxIcon.Information
);
}
private void textBox1_KeyPress(object sender, KeyPressEventArgs e)
{
if (e.KeyChar == 8) return;//wyskocz na BackSpace
if (e.KeyChar < '0' || e.KeyChar > '9') e.Handled = true;//ignoruj nienumeryczne
}
}
}









