Ciąg Fibonacciego

Ciąg liczb naturalnych spełniający zależność:

ciąg zaczyna się od liczby 1 oraz 1, każda kolejna liczba ciągu to suma dwóch poprzednich.

Początkowe wyrazy ciągu:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 itd.

Zapis definicji ciągu Fibonacciego

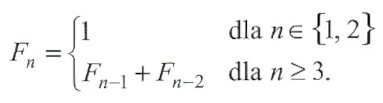
Przykładowy problem obliczenia populacji królików

Ile królików będzie po 24 miesiącach przy założeniu że:

żaden królik nie zdechnie w ciągu badanego okresu czasu
każda para królików wydaje na świta co miesiąc kolejną parę królików

Schemat liczebności królików ciąg fibonacciego

Źródło Informatyka dla szkół ponadpodstawowych. Zakres podstawowy Klasa II wyd. MiGra

Schemat algorytmu obliczającego n pierwszych wyrazów ciągu Fibonacciego- rozwiązanie iteracyjne

Kod ciała funkcji realizujący iteracyjne wyznaczanie liczb ciągu Fibonacciego

Wskazówka:


	void fibIteracja(int n, TextBox tb)
	{
		Int64 a=0,b=1;
		for (int i = 0; i < n; i++)
		{
			tb.AppendText(b.ToString() + Environment.NewLine);
			b += a;
			a = b - a;
		}
	}

Schemat algorytmu obliczającego n pierwszych wyrazów ciągu Fibonacciego- rozwiązanie rekurencyjne

Schemat algorytmu obliczającego n pierwszych wyrazów ciągu Fibonaciego- rozwiązanie rekurencyjne. Visual studio C#

Kod ciała funkcji realizujący rekurencyjne wyznaczanie liczb ciągu Fibonacciego

Wskazówka:


	int fibRekurencja(int n)
	{
		if (n < 3) return 1;
		return fibRekurencja(n - 2) + fibRekurencja(n - 1);
	}

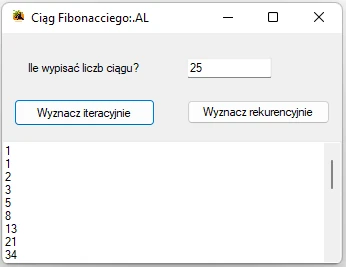
Przykładowa aplikacja zapisana w Visual Studio C# wyznaczająca n wyrazów ciągu Fibonacciego metodą iteracyjną i rekurencyjną

Pełny kod klasy Form utworzonej formatki dla powyższej aplikacji

Wskazówka:

 
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace _7AlgFibonacci
{
    public partial class Form1 : Form
    {
        void fibIteracja(int n, TextBox tb)
        {
            Int64 a=0,b=1;
            for (int i = 0; i < n; i++)
            {
                tb.AppendText(b.ToString() + Environment.NewLine);
                b += a;
                a = b - a;
            }
        }
        int fibRekurencja(int n)
        {
            if (n < 3) return 1;
            return fibRekurencja(n - 2) + fibRekurencja(n - 1);
        }

        public Form1()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            if (textBox2.Text.Length < 1) return;
            textBox1.Clear();
            int n = int.Parse(textBox2.Text);
            fibIteracja(n, textBox1);
        }

        private void button2_Click(object sender, EventArgs e)
        {
            if (textBox2.Text.Length < 1) return;
            textBox1.Clear();
            int n = int.Parse(textBox2.Text);
            for(int i=1;i<=n;i++)
               textBox1.AppendText(fibRekurencja(i).ToString()+Environment.NewLine);
        }

        private void textBox2_KeyPress(object sender, KeyPressEventArgs e)
        {
            if (e.KeyChar == 8) return;//wyskocz jak BackSpace
            if(e.KeyChar<'0'||e.KeyChar>'9') e.Handled = true;
        }

        
    }
}