Obliczanie pola obszarów zamkniętych metodą trapezów i prostokątów- algorytm całkowania
Obliczanie pola obszarów zamkniętych w ujęciu numerycznym polega na odpowiednim dopasowaniu ilości pól prostokątów lub trapezów o takiej podstawie i wysokości aby nie wychodziły poza obszar ograniczony linia krzywej, dla której znamy funkcję opisującą jej przebieg. Obliczanie tą metodą wartości pola odpowiada całkowaniu. Wartość otrzymanego wyniku jest tym lepsza im lepsze jest dopasowanie prostokątów lub trapezów. Ten sposób całkowania numerycznego polegający na zastąpieniu całki oznaczonej przez przybliżoną wartość sumy zwane jest kwadraturą.
Metoda prostokątów

Dopasowanie pola prostokątów najlepiej sprawdza się gdy przy ustaeleniu szerokości podstawy prostokąta bierzemy pod uwagę dopasowanie wysokości prostokąta w połowie przedziału. Na rysunku czerwona przerywana linia.
Ilość prostokątów ustalamy przez podanie liczby przedziałów w granicy przedziału [a,b]. Zapis wzorem wartości pola pod krzywą f(x) w przedziale [a,b] wyrazi się tak zwanym wzorem prostokątów

Metoda trapezów
Metoda trapezów obliczania wartości pól pod krzywą f(x) bazuje na tym samym pomyśle co metoda prostokątów. Metoda trapezów różni się od metody prostokątów tym, że daje dokładniejszy wynik sumowania. Wiąże się to z dokładniejszym dopasowaniem

Wartość sumowania metodą trapezów opisuje poniższy wzór

Schemat algorytmu całkowania numerycznego metodą prostokątów
W działaniach przedstawionych na poniższym schemacie algorytmu całkowania numerycznego metodą prostokątów pod symbolem f(sr) rozumie się wartość zadanej funkcji dla argumentu środka przedziału wyznaczającego podstawę kolejnego prostokąta.

Uwaga: Jeżeli chcemy obliczyć wartość pola ograniczonego krzywą, to w funkcji obliczającej jej wartość dla podanego argumentu stosujemy wartość bezwzględną (Math.Abs). Wtedy ewentualna część ujemna pod wykresem będzie dodatnia. W przypadku obliczania numerycznego całki nie należy tego stosować.
Przykładowy kod funkcji dla algorytmu całkowania numerycznego metoda prostokątów zapisany w języku C#
Wskazówka:
float mProstokatow(float a,float b,int n)
{
//wszystki eprostokąty mozna zastapić jednym o sumie wysokości każdego
//i podstawie pojedynczego, pole takiego prostokata bedzie polem całki
float dx = (b - a) / (float)n,//oblicz podstawe prostokatów
h = 0,//bieżąca wysokosci
sr = a + (b - a) / (2.0f * n);//srodek pierwszego prostokata
for(int i = 0; i < n; i++)
{
h = h + f(sr);//zwieksz wysokość
sr = sr + dx;//wzynacz kolejny srodek
}
return h*dx;
}
Schemat algorytmu całkowania numerycznego metoda trapezów

Kod funkcji napisany w języku C# według algorytmu całkowania numerycznego metodą trapezów
Wskazówka:
float mTrapez(float a, float b, int n)
{
float dx =(b-a)/(float)n,//bieżąca podstawa trapezow
da = f(a),//biezacy bok a
db,//biezacy bok b
h=0;//biezaca wysokosc
for(int i = 1; i <= n; i++)
{
//licz biezacy bok b trapezu
db = f(a + dx * i);
h = h + (db + da);
//ustal nowy bok a
da = db;
}
return h * 0.5f*dx;
}
Dla obu powyższych kodów wykorzystana jest funkcja obliczające pole pod krzywą daną wzorem f(x)=x3-36
Przykład aplikacji liczącej pole pod krzywą wykorzystując całkowani numeryczne metodą prostokątów i trapezów
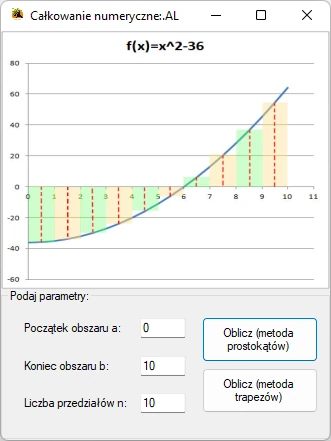
Pełny kod klasy Form dla formatki utworzonej aplikacji
Form1.cs
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace _20AlgCalkowanieNumeryczne
{
public partial class Form1 : Form
{
float f(float x)
{
//obliczenia dla funkcji
//zadanej wzorem f(x)=x^2-36
//gdyby byla liczona wartość całki
//to pomiń wartość bezwzględną
return Math.Abs(x * x - 36);
//całka x^3/3-36
}
float mProstokatow(float a,float b,int n)
{
//wszystki eprostokąty mozna zastapić jednym o sumie wysokości każdego
//i podstawie pojedynczego, pole takiego prostokata bedzie polem całki
float dx = (b - a) / (float)n,//oblicz podstawe prostokatów
h = 0,//bieżąca wysokosci
sr = a + (b - a) / (2.0f * n);//srodek pierwszego prostokata
for(int i = 0; i < n; i++)
{
h = h + f(sr);//zwieksz wysokość
sr = sr + dx;//wzynacz kolejny srodek
}
return h*dx;
}
float mTrapez(float a, float b, int n)
{
float dx =(b-a)/(float)n,//bieżąca podstawa trapezow
da = f(a),//biezacy bok a
db,//biezacy bok b
h=0;//biezaca wysokosc
for(int i = 1; i <= n; i++)
{
//licz biezacy bok b trapezu
db = f(a + dx * i);
h = h + (db + da);
//ustal nowy bok a
da = db;
}
return h * 0.5f*dx;
}
public Form1()
{
InitializeComponent();
}
private void textBox1_KeyPress(object sender, KeyPressEventArgs e)
{
//wyskocz na BackSpcae, Enter lub minus
if (e.KeyChar == 8 || e.KeyChar == 13 || e.KeyChar == '-') return;
if (e.KeyChar < '0' || e.KeyChar > '9') e.Handled = true;//blokuj nienumeryczne
}
private void textBox3_KeyPress(object sender, KeyPressEventArgs e)
{
//wyskocz na BackSpcae, Enter lub minus
if (e.KeyChar == 8) return;
if (e.KeyChar < '0' || e.KeyChar > '9') e.Handled = true;//blokuj nienumeryczne
}
private void button1_Click(object sender, EventArgs e)
{
if (textBox1.Text.Length < 1
|| textBox2.Text.Length < 1
|| textBox3.Text.Length < 1) return;
float a = float.Parse(textBox1.Text),
b = float.Parse(textBox2.Text);
int n = int.Parse(textBox3.Text);
MessageBox.Show(
mProstokatow(a,b,n).ToString(),
"Wartość pola (met. prostokątów):",
MessageBoxButtons.OK,
MessageBoxIcon.Information
);
}
private void button2_Click(object sender, EventArgs e)
{
if (textBox1.Text.Length < 1
|| textBox2.Text.Length < 1
|| textBox3.Text.Length < 1) return;
float a = float.Parse(textBox1.Text),
b = float.Parse(textBox2.Text);
int n = int.Parse(textBox3.Text);
MessageBox.Show(
mTrapez(a, b, n).ToString(),
"Wartośc pola (met. trapezow):",
MessageBoxButtons.OK,
MessageBoxIcon.Information
);
}
}
}









