Algorytm szybkiego potęgowania

Przykładowo najprostsze podejście do obliczenia potęgi dla x⁹

x⁹=x⋅x⋅x⋅x⋅x⋅x⋅x⋅x⋅x jest równoznaczne z wykonaniem 8 mnożeń

Można skrócić ilość wykonywanych mnożeń przez buforowanie wyniku wcześniej wykonanego iloczynu

• x² mnożenie 1, czyli x⋅x=x²
• (x²)⋅ ( x²) mnożenie 2
• (x⁴)⋅ ( x⁴) mnożenie 3
• x⁸⋅x mnożenie 4, cztery tak wykonane mnożenia to x⁹

Ten sposób potęgowania był znany w Indiach już od około 200 roku p.n.e

Jak zmusić maszynę aby tak potęgowała?

Stosując binarne rozwiniecie wykładnika potęgi można bardzo znacznie przyśpieszyć obliczenie potęgi o dowolnym wykładniku. Liczbę 9 w tym wypadku nasz wykładnik można przedstawić tak: 9=(1001)₂

• najbardziej znaczący bit w rozwinięciu wykładnika odpowiada rozpoczęciu obliczeń od przyjęcia liczby za początkową wartość potęgi
• każda następna pozycja w rozwinięciu odpowiada podniesieniu częściowego wyniku do kwadratu i ewentualnie pomnożenie przez x, jeśli bit rozwinięcia na tej pozycji jest równy 1

Przyjmując oznaczenia: P- potęgowanie, X - mnożenie to w miejsce każdej JEDYNKI za wyjątkiem bitu najstarszego wstawiamy symbol PX (potęguj i mnóż), zaś za każdy bit ZEROWY wstawiamy symbol P (potęguj) otrzymamy taki zapis

1001 >symbolicznie> PPPX, ten zapis odpowiada wykonaniu 4 mnożeń

Realizując potęgowanie w kodzie programu można jego budowę usprawnić wykorzystując fakt, że zamiana liczby dziesiętnej na jej rozwinięcie binarne odbywa się od bitu najmniej znaczącego - od końca. Czyli od PRAWEJ DO LEWEJ

Kroki algorytmu szybkiego potęgowania

Dane: Podstawa potęgi - liczba a, wykładnik potęgi - liczba n

Wynik: Wartość potęgi w=aⁿ

Krok 1

Przyjmij wynik w=1

Krok 2

Jeśli kolejny bit liczony od prawej strony rozwinięcia binarnego wykładnika potęgi wynosi 1, to zwiększ wynik X razy;

Czyli

Jeśli n % 2 == 1 to w=w⋅a

Krok 3

Dopóki n>0 przypisz n = n/2; jeśli n==0 to zakończ algorytm

Krok 4

Wykonaj potęgowanie a=a⋅ a; Wróć do kroku 2

UWAGA: Sprawdzenie czy rozwinięci binarne wykładnika zawiera bit o wartości 1, to w wyżej wymienionych krokach jest wykonanie dzielenia z resztą przez dwa (n % 2 = = 1)

Schemat algorytmu szybkiego potęgowania (metoda iteracyjna)

Kod funkcji realizującej algorytm szybkiego potęgowania metodą iteracyjną zapisany w języku C#

long potIteracja(int a,int n)
{
	long w = 1;//wynik, wstępnie równy 1
	while (n > 0)
	{
		if (n % 2 == 1)w = w*a;
		a = a * a;
		n = n/2;
	}
	return w;
}

Schemat algorytmu szybkiego potęgowania (metoda rekurencyjna)

Kod funkcji realizującej algorytm szybkiego potęgowania metodą rekurencyjną zapisany w języku C#

long potRekurencja(int a, int n)
{
	if (n == 0) return 1;
	//przypadek gdy n jest nieparzyste
	if(n%2 == 1) return a*potRekurencja(a,n-1);
	//dla n parzystego
	long w = potRekurencja(a, n / 2);
	return w * w;
}

Przykładowa aplikacja wykorzystująca algorytm szybkiego potęgowania

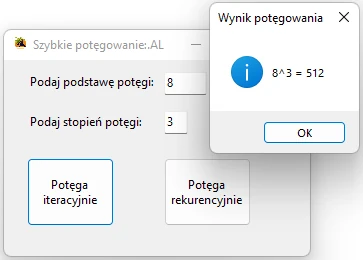
Pełny kod klasy Form utworzonej formatki dla wyżej wymienionej aplikacji

namespace _18AlgSzybkiePotegowanie
{
    public partial class Form1 : Form
    {
        int a;//podstawa potęgi
        int n;//stopień potęgi
        
        long potIteracja(int a,int n)
        {
            long w = 1;//wynik, wstępnie równy 1
            while (n > 0)
            {
                if (n % 2 == 1)w = w*a;
                a = a * a;
                n = n/2;
            }
            return w;
        }

        long potRekurencja(int a, int n)
        {
            if (n == 0) return 1;
            //przypadek gdy n jest nieparzyste
            if(n%2 == 1) return a*potRekurencja(a,n-1);
            //dla n parzystego
            long w = potRekurencja(a, n / 2);
            return w * w;
        }

        public Form1()
        {
            InitializeComponent();
        }

        private void textBox1_KeyPress(object sender, KeyPressEventArgs e)
        {
            //wyskocz na BackSpcae
            if (e.KeyChar == 8) return;
            if (e.KeyChar < '0' || e.KeyChar > '9') e.Handled = true;//blokuj nienumeryczne
        }

        private void button1_Click(object sender, EventArgs e)
        {
            if (textBox1.Text.Length < 1 || textBox2.Text.Length < 1) return;
            a = Int32.Parse(textBox1.Text);
            n = Int32.Parse(textBox2.Text);
            MessageBox.Show(
                a.ToString() + "^" +n.ToString()
                + " = " + potIteracja(a, n).ToString(),
                "Wynik potęgowania",
                MessageBoxButtons.OK,
                MessageBoxIcon.Information
                );
        }

        private void button2_Click(object sender, EventArgs e)
        {
            if (textBox1.Text.Length < 1 || textBox2.Text.Length < 1) return;
            a = Int32.Parse(textBox1.Text);
            n = Int32.Parse(textBox2.Text);
            MessageBox.Show(
                a.ToString() + "^" + n.ToString()
                + " = " + potRekurencja(a, n).ToString(),
                "Wynik potęgowania",
                MessageBoxButtons.OK,
                MessageBoxIcon.Information
                );
        }
    }
}